Hash函数

Hash函数计算的是一个消息的摘要，并且这个摘要是一个非常短、长度固定的位字符串。对某个特定的消息而言，消息摘要（或哈希值）可以看作是该消息的指纹，即消息的唯一表示。

Hash函数是一种没有密钥的加密方法，没有密钥证明Hash函数是不可逆的，即从实际计算角度出发，根据密文不能得出实际明文（因为受限于当前的计算能力，Hash结果的破解需要很长很长的时间，所以是计算不可行）。

Hash函数主要应用在数字签名和消息验证码。

为什么数字签名需要Hash函数？

之前介绍的非对称加密与数字签名
中提到过数字签名的签名生成与验证均是作用于明文数据的哈希值，为什么要这样呢？因为在所有的签名方案中（主要三大类：大素数因式分解难（RSA）、离散对数（Elgamal）以及椭圆曲线（ECC）），明文的长度都是有限的，例如在RSA中，消息长度通常在1024位～3072位之间
（128字节～384字节），但实际应用中明文长度通常超过这个范围很多，所以需要解决明文长度问题，而Hash函数便是一种解决方案。Hash函数签名过程如下图：

注意：在实际签名与验证签名的过程中，作用对象都是实际明文的哈希值，而非明文本身

Hash函数的安全性

对于Hash函数，以下三点属性需要了解：

要想对任意大小的消息使用哈希函数，则哈希函数在计算上必须是高效的，即使消息大小有几百MB。
哈希函数的输出长度是固定的，即对同一个哈希函数，无论消息长度是多少，哈希函数的输出长度总是固定的。
哈希函数必须对所有的输入位都高度敏感，即使输入发生了很小的改变，哈希函数的输出也有很大的不同。

如下图：

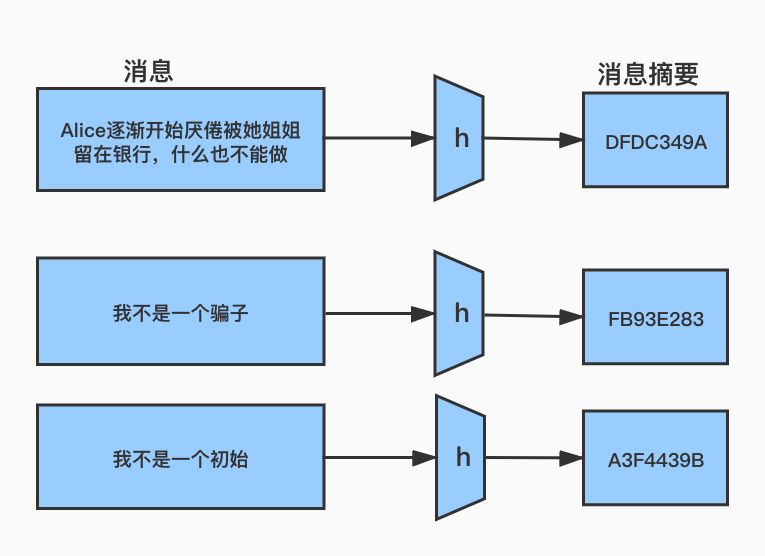
为了保证安全性，Hash函数还需要拥有以下三个核心属性：

抗第一原像性（或单向性）

哈希函数必须具有单向性，即给定一个哈希输出z，找到满足z = h(x)的输入消息x在计算上必须是不可行的，即给定一个指纹，我们不可能找到对应的消息。
抗第二原像性（或弱抗冲突性）

对使用哈希的数字签名而言，确保两个不同的消息不会映射到相同的值是非常重要的，明确的说就是使用相同的哈希值$z_1$ = h($x_1$) = h($x_2$) = $z_2$创建两个不同的消息$x_1$ != $x_2$在计算上是不可行的。

给定明文$x_1$，弱冲突性就是存在$x_2$的哈希值与$x_1$相同，这在理论上是可行的，这里有一个有趣的原理，叫鸽巢原理：如果你有100只鸽子，却只有99个笼子，则至少有一个鸽笼会装两个鸽子。由于Hash函数的输
出长度都是固定的，而输入的数目没有限制，所以一定会存在多个输入哈希到相同输出值的情况。但是因为哈希输出长度（比如80位）在计算上如果要计算出相同的输入，目前的计算能力需要很长的时间，所以实际应用中可
以认为是安全的，但是随着计算能力的提升，对应Hash的输出长度也会增加，这样就衍生衍生出了很多不同算法的Hash函数，对应的输出长度也不尽相同。
抗冲突性（或强抗冲突性）

只有当找不到满足h($x_1$) = h($x_2$)的$x_1$，$x_2$时，哈希函数才是抗冲突或具有强抗冲突性，这个属性比弱抗冲突性更难获得，因为攻击者具有两方面的自由：可以更改两个消息以获得相似的哈希值。这里也有一个
有趣的理论，叫做生日悖论，大概描述的是：至少需要多少人聚会，才能使得至少两个人拥有相同生日的概率足够高？有兴趣的话可以去详细了解以下。

基于以上内容，Hash函数具有以下属性：

1. 任意的消息大小： h(x)对任何大小的消息x都适用

2. 固定的输出长度： h(x)生成的哈希值z的长度是固定的

3. 有效性： h(x)的计算相对简单

4. 抗第一原像性： 给定一个输出z，找到满足h(x) = z的输入x是不可能，即h(x)具有单向性

5. 抗第二原像性： 给定$x_1$和h($x_1$)，找到满足h($x_1$)=h($x_2$)的$x_2$在计算上是不可能的

6. 抗冲突性： 找到满足h($x_1$)=h($x_2$)的一对$x_1$ != $x_2$ 在计算上是不可行的

Hash函数的构建以及分类

从构建方式来看，Hash函数主要分为两类:

专用的Hash函数，专门为Hash函数设计的一些算法
基于分组密码的Hash函数

Hash函数的实质是将任意长度的消息转换称固定长度的输出，所以Hash函数的核心功能是压缩，输入消息的哈希值可以定义为上一轮压缩函数的输出，如下图所示：

关于算法理论细节请参考书籍上更详细的内容，本文内容参考《深入浅出密码学——常用加密技术原理与应用》

哈希函数主要分类如下图所示:

上图内容引《自维基百科》

Hash函数实践(Golang)

package main

import (
    "crypto"
    "fmt"
    "github.com/pyihe/secret"
)

func main() {
    data := []byte("明文数据")
    s := secret.NewHasher()
    hash, err := s.HashToBytes(data, crypto.SHA256)
    if err != nil {
        fmt.Printf("exit with err: %v\n", err)
        return
    }
    base64Str, err := s.DoubleHashToString(data, crypto.SHA256)
    if err != nil {
        fmt.Printf("exit with err: %v\n", err)
        return
    }
    fmt.Printf("bytes result: %s\n", hash)
    fmt.Printf("string result: %s\n", base64Str)
}

消息验证码

消息验证码（MAC）也称为密码学校验和或密钥的哈希函数。在安全功能方面，MAC与数字签名共享一些属性，因为它们都提供消息完整性和消息验证，但是与数字签名不同的是，MAC是对称密钥方案，并且它也不提供不可否认性。

与数字签名一样，MAC也是将验证标签附加到消息后面，MAC与数字签名最大的区别就是，MAC在生成和确认验证标签的过程中使用的都是对称密钥K，即：m = $MAC_k$(x)，MAC流程如下图所示：

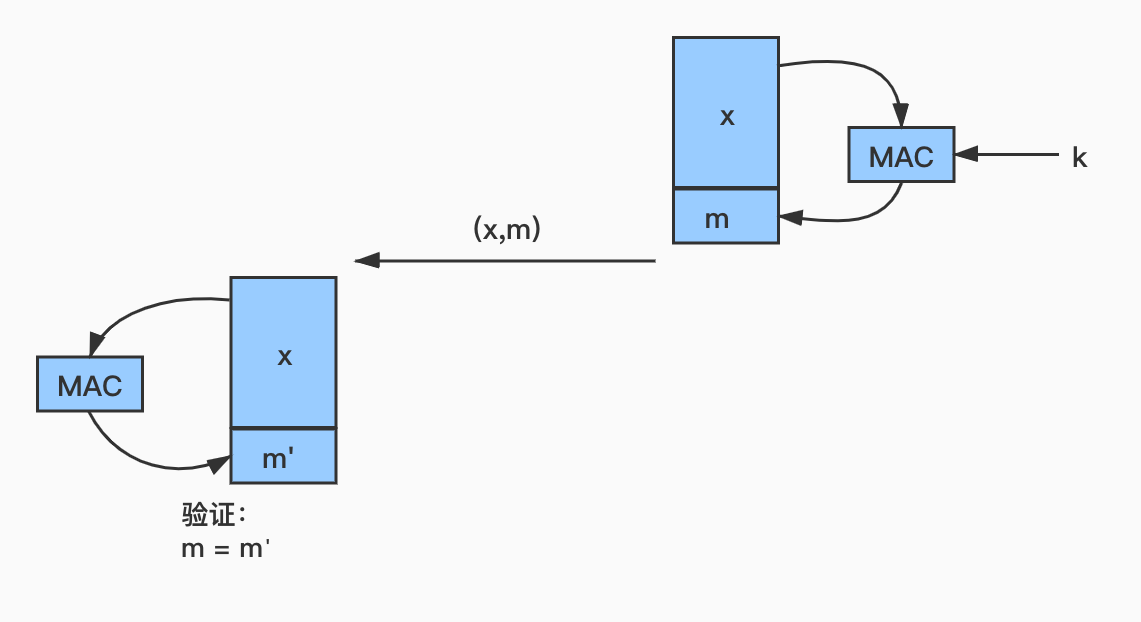
发送方计算出MAC，并将消息和验证标签m一起发送给接收方，接收方收到消息x和m时将这两者进行验证，验证与发送方的操作完全相同：使用收到的消息和对称密钥重新计算并认证即可。

消息验证码具有以下属性：

1. 密码学校验和： 给定一个消息，MAC可以生成一个密码学安全的验证标签

2. 对称性： MAC基于对称密钥，签名方和验证方必须共享一个密钥

3. 任意的消息大小： MAC可以接受任意长度的消息

4. 固定的输出长度： MAC生成固定长度的验证标签

5. 消息完整性： MAC提供了消息完整性，在传输过程中对消息的任何修改都能被接收者检测到

6. 消息验证： 接收方可以确定消息的来源

7. 不具有不可否认性： 由于MAC是基于对称原理的，所以不提供不可否认性，即无法向第三方证明消息来自发送方还是接收方

HMAC

HMAC是MAC的一种实现方案，由一个内部哈希和一个外部哈希组成，如下图所示：

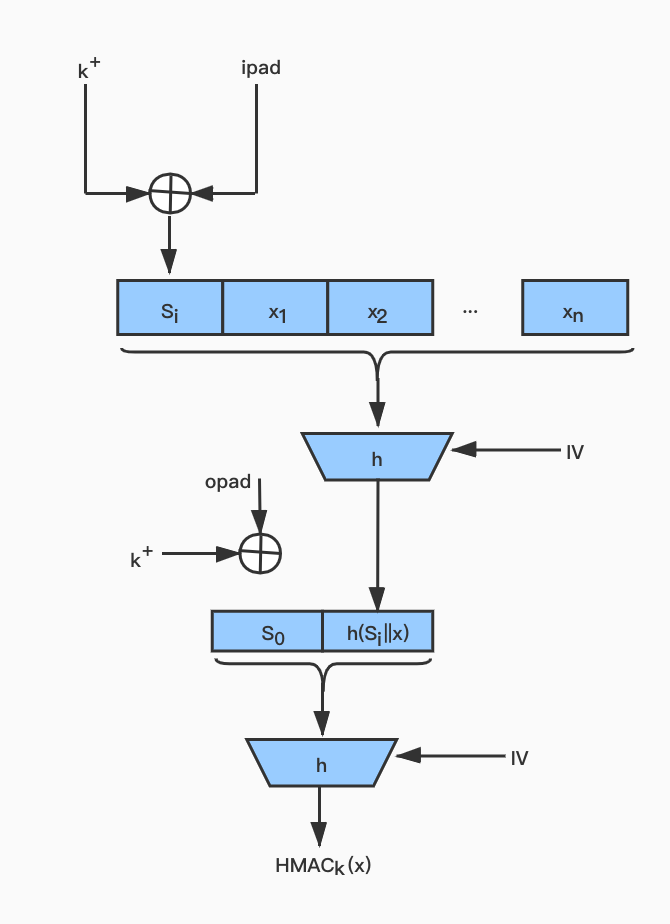
图中||表示连接。MAC计算首先使用0在对称密钥k的左边进行填充，直到得到的$k^+$的长度为b位，其中b是哈希函数输入分组的宽度。扩展后的密钥然后与内部填充进行异或操作，直到达到长度b，其中内部填充是由下位模式的重复组成的：

ipad = 0011 0110, 0011 0110, ..., 0011 0110

异或操作的输出形成了哈希函数的第一个输入分组。后续的输入分组为消息分组($x_1$, $x_2$, …, $x_n$)。

使用填充的密钥与第一个哈希的输出一起计算出第二个外部哈希，这里的密钥也需要使用0进行填充，并与外部填充进行异或操作：

opad = 0101 1100, 0101 1100, ..., 0101 1100

异或操作的结果形成了外部哈希的第一个输入分组，其他输入分组为内部哈希的输出。计算完外部哈希得到的输出就是x的消息验证码。

消息验证码实践(Golang)

package main

import (
    "crypto"
    "fmt"
    "github.com/pyihe/secret"
)

func main() {
    data := []byte("明文数据")
    key := []byte("12345678")
    s := secret.NewHasher()
    mac := s.MAC(crypto.SHA512, data, key)
    ok := s.CheckMac(crypto.SHA512, data, key, mac)
    fmt.Println(ok)
}

最后

如有错误，欢迎指正！

Thanks!

附上代码链接[github.com/pyihe/secret]

星星点灯

加密算法之Hash函数与消息验证码