树结构
树
树结构是由一个父节点以及若干个子节点,然后子节点又是其他子节点的父节点,由此而形成的一种结构即是树。其中节点的子节点的子节点叫做该节点的孙节点。如下所示:
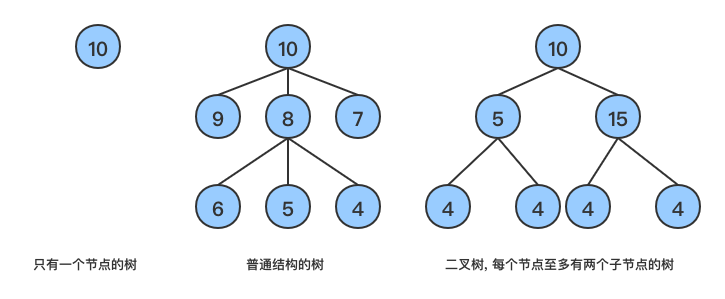
二叉树(Binary Tree, BT)
二叉树是树结构的应用形式之一,二叉树每个节点至多有两个子节点,如上面第三个树结构所示,位于左边的子节点叫做左孩子或者左子节点,位于右边的叫做右孩子或者右子节点。
二叉搜索(查找)树(Binary Search Tree, BST)
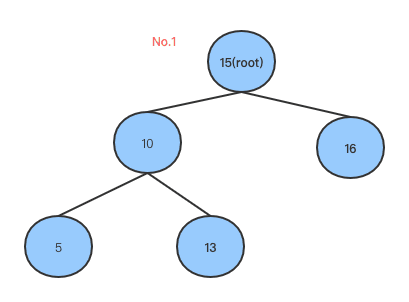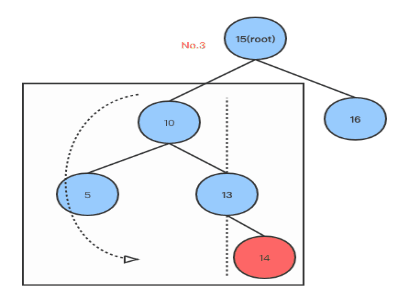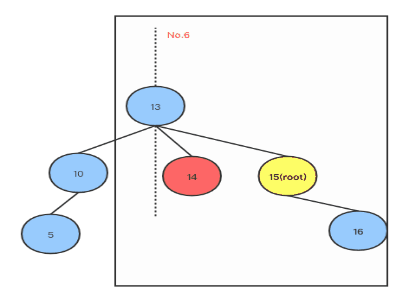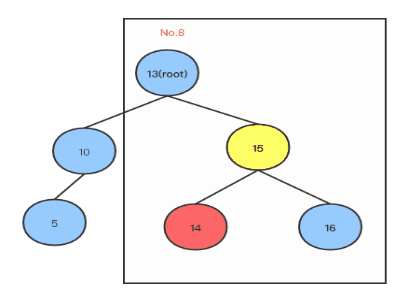
二叉搜索树是二叉树的应用之一,在一棵二叉搜索树中,父节点的值总是小于(或者大于)左孩子,而右孩子的值总是大于(或者小于)父节点,由此便构成了一棵有序的树结构。如下图所示:

平衡二叉树(AVL)
二叉搜索树是一棵有序的树,但是大多数情况下,往二叉搜索树中插入节点时,可能存在的情况是插入的节点始终位于一个分支上,如下图所示:
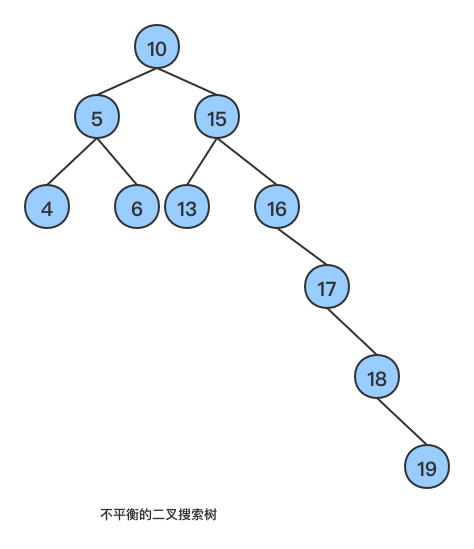
这样就出现了一种不尽如人意的情况,就是在一棵二叉搜索树中,某一个分支节点很少,而另一个分支上节点却很多,导致在查找、插入、删除等操作上效率很低。
在一棵二叉搜索树中,对于某一个节点,如果该节点左子树和右子树的高度差的绝对值超过了
abs(h) > 1,则称该树为非平衡二叉搜索树。为了改善这种情况,便出现了平衡二叉树,顾名思义,平衡二叉树任意一个节点的左子树和右子树高度差的绝对值都abs(h)<=1。平衡二叉树是在二叉搜索树的基础上,增加了平衡二叉树的操作,使得二叉搜索树是一棵平衡树。如下图为一棵平衡二叉树: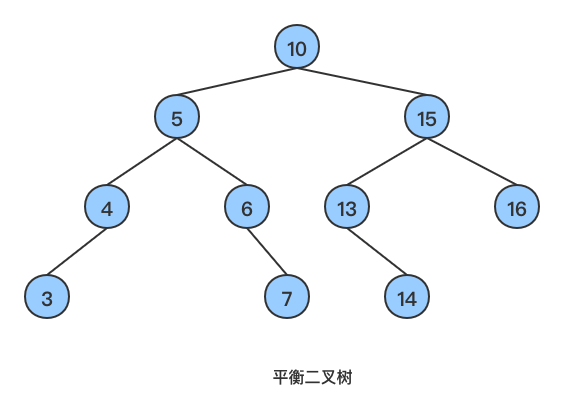
平衡查找树的平衡
前面已经提到什么是平衡二叉树,那么怎么样形成一棵平衡的二叉树呢?
权威们给出的答案是旋转,即通过对二叉树进行旋转来改变树的结构并且不改变节点值的顺序,从而得到一棵平衡的二叉树。下面介绍树的旋转,树的旋转分为左旋转、右旋转以及左右旋转,右左旋转。
因为树的节点个数变化为1、2、3…n,所以当节点总数小于3时一棵二叉搜索树一定是平衡的,如下图:
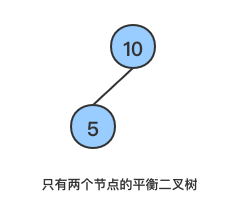
此时左子树的高度与右子树的高度差的绝对值为1,所以是平衡的(在下文中提到的高度差都是左子树高度减去右子树高度)。但是随着节点的插入,有可能变成不平衡的了。以下为需要旋转操作进行平衡二叉树的情况,均是针对最少节点数的情况,即需要旋转操作的最小子树。
注: 下文提到的高度差均为左子树减去右子树的高度差的绝对值,同时本文中的平衡二叉树为左节点小于父节点,父节点小于右节点
左旋转
在右子树添加节点造成不平衡。root只有右孩子的情况,以root的右孩子为中心,向左(逆时针)旋转root节点,旋转结果为root节点变为root右孩子的左孩子,如下图:

在右子树添加节点(图中的16),造成不平衡。
在右子树添加节点造成不平衡,其中root同时有左右子树,左子树只有一个节点,右孩子只有一个右子节点,添加一个节点(下图中的17)后造成不平衡树,此时可以看到,root的右子树不平衡,此时按照第一种旋转方式可以将右子树旋转平衡,进而使整棵树平衡,如下图:

在右子树添加节点造成不平衡,其中root只有一个左孩子,root的右孩子同时存在左右孩子,如下图:
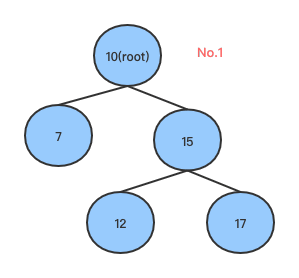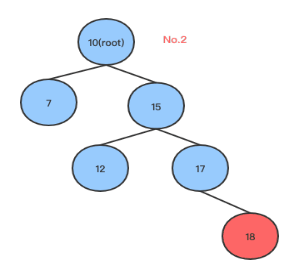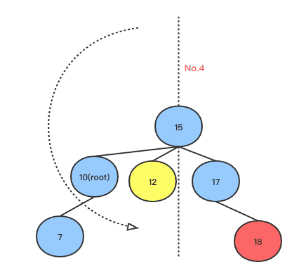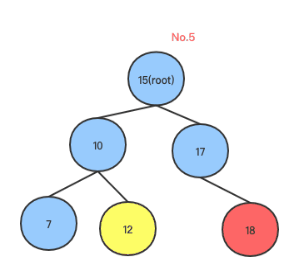
从上面可以看出,如果root右子树比左子树高2,并且右子树的右子树比右子树的左子树高,则执行左旋转,以下是左旋转的代码(Golang):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46type Element interface {
Value() interface{}
Compare(Element) int //相等返回0,小于返回负数,大于返回正数
}
type AVLNode struct {
Data Element //存放的元素
Height int //存放节点的高度
Left *AVLNode //左子树
Right *AVLNode //右子树
}
func (avl *AVLNode) Max() *AVLNode {
node := avl
for node.Right != nil {
node = node.Right
}
return node
}
func getHeight(avl *AVLNode) int {
if avl != nil {
return avl.Height
}
return 0
}
func maxHeight(h1, h2 int) int {
if h1 > h2 {
return h1
}
return h2
}
func leftRotate(avl *AVLNode) *AVLNode {
if avl == nil {
return nil
}
node := avl.Right
avl.Right = node.Left
node.Left = avl
avl.Height = maxHeight(getHeight(avl.Left), getHeight(avl.Right)) + 1
node.Height = maxHeight(getHeight(node.Left), getHeight(node.Right)) + 1
return node
}右旋转
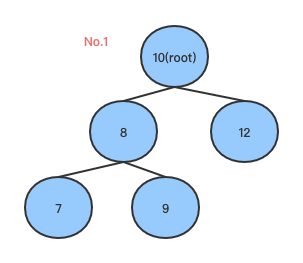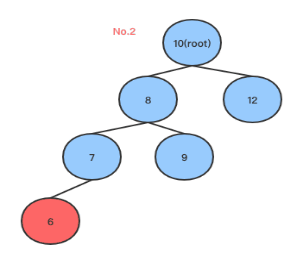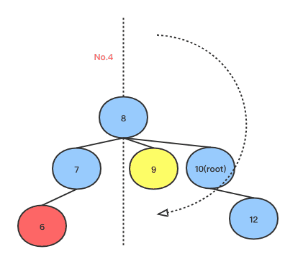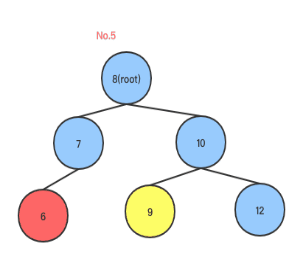
在左子树添加节点造成不平衡, root没有右孩子,同时左孩子只有左孩子一个节点, 此时以root的左孩子为中心,进行右旋转(顺时针旋转), 将root左孩子提升为root,root降为左孩子的右孩子,如下图:

在左子树添加节点造成不平衡, root同时包含左右孩子,右孩子没有子节点,左孩子只有一个左孩子节点,此时root的左子树为不平衡树,按照上面的方式对左子树进行右旋转得到平衡树,如下图:

在左子树添加节点造成不平衡, root只有一个右孩子, 左孩子同时有左右孩子, 在左孩子的左孩子下添加一个节点, 如下图:
从上面可以看出, 如果root左子树比右子树高2,并且左子树的左子树比左子树的右子树高,则执行右旋转,以下是右旋转的代码(Golang):
1
2
3
4
5
6
7
8
9
10
11
12
13func rightRotate(avl *AVLNode) *AVLNode {
if avl == nil {
return nil
}
node := avl.Left //左子树
avl.Left = node.Right //左子树的右子树变为左子树
node.Right = avl //avl降为左子树的右子树
//更新节点高度
avl.Height = maxHeight(getHeight(avl.Left), getHeight(avl.Right)) + 1
node.Height = maxHeight(getHeight(node.Left), getHeight(node.Right)) + 1
return node
}左右旋转
左右旋转是指先执行左旋转再执行右旋转。
在左子树添加节点造成不平衡,root只有左子树,且左子树只有一个节点,如下图:

在左子树添加节点造成不平衡,root同时有左右孩子,root的左孩子同时有左右孩子,在root的左孩子的右孩子上添加左节点造成不平衡,如下图:

在左子树添加节点造成不平衡,root同时有左右孩子,root的左孩子同时有左右孩子,在root的左孩子的左孩子上添加右节点造成不平衡,如下图:
从上面可以看出, 如果root左子树比右子树高2,并且左子树的右子树比左子树的左子树高2,则先执行左旋转,再执行右旋转,以下是左右旋转的代码(Golang):
1
2
3
4
5//先将左孩子左旋转,自己再右旋转
func (avl *AVLNode) leftRightRotate() *AVLNode {
avl.Left = avl.Left.leftRotate()
return avl.rightRotate()
}右左旋转
右左旋转是指先执行右旋转再执行左旋转。
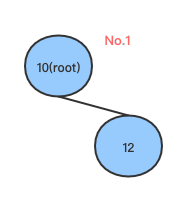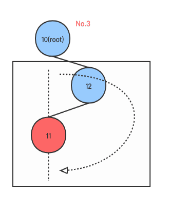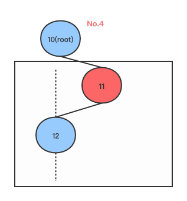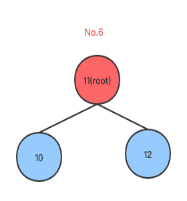
在右子树添加节点造成不平衡, root只有右子树,且右子树只有一个节点,如下图:
在右子树添加节点造成不平衡, root同时有左右孩子,root的右孩子同时有左右孩子,在root的右孩子的左孩子上添加右节点,如下图:

在右子树添加节点造成不平衡, root同时有左右孩子,root的右孩子同时有左右孩子,在root的右孩子的左孩子上添加左节点,如下图:
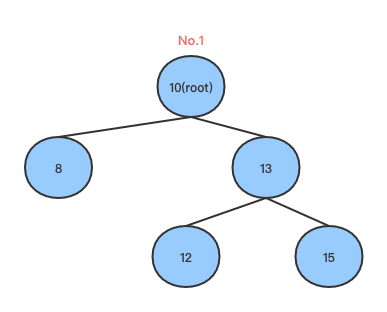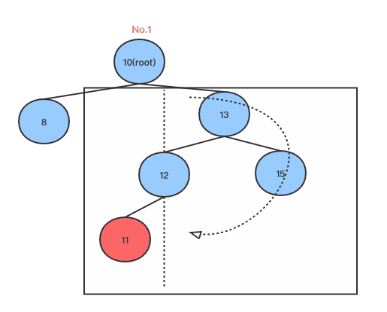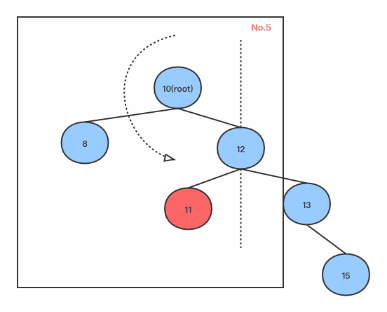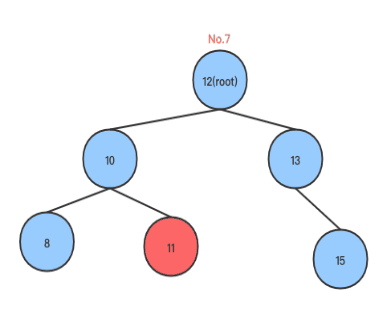
从上面可以看出, 如果root右子树比左子树高2, 并且右子树的右子树比右子树的左子树矮, 则执行右旋转后再执行左旋转,以下是左右旋转的代码(Golang):
1
2
3
4
5//先将右孩子右旋转,然后自己右旋转
func (avl *AVLNode) rightLeftRotate() *AVLNode {
avl.Right = avl.Right.rightRotate()
return avl.leftRotate()
}
综上可以得出平衡二叉查找树的函数为:
1 | //调整树为二叉平衡树 |
插入、删除节点
以上为树的旋转操作,用于平衡二叉查找,对于二叉查找树,每添加或者插入一个节点后均需要执行一次平衡操作。代码如下:
1 | //添加节点 |
最后
谢谢!